![[CSAPP] Datalab :: Bit Counting Algorithms (bitCount, countOneBits)](https://tistory1.daumcdn.net/tistory/4291665/attach/12233fcdcabc492b82a733756a9fb0c4)
아래의 내용들은 시스템 프로그래밍(CS230; CSAPP)를 수강할 때 lab session을 진행하면서 얻은 알고리즘을 정리했습니다. 이 글에서는 비트 세기 알고리즘, Bit Counting Algorithm에 대해서 알아보려고 합니다. 이 글에서는 알고리즘의 개념에 대해서 설명하고 자세한 코드는 다른 글을 통해서 설명하겠습니다. Bit Counting Algorithm은 선형적인 방법(linear)과 이분적인 방법(binary)가 있으니, 이를 구분해서 글을 읽으면 도움이 될 것입니다. Binary algorithm은 3. Neighbor Counting과 4. Cross Counting 을 소개합니다. 연산자 개수 단축을 위해서 datalab을 해결할 때에는 두 알고리즘을 사용해야 합니다.
일부 랩에서 bitCount 또는 countOneBits라고도 불리는 문제입니다. 똑같이 1의 개수를 세는 문제이기에 차이는 없습니다.
코드는 맨 아래에 있습니다.
글이 알고리즘을 세세하게 설명하니, 각 단계별로 그려둔 figure를 기반으로 먼저 이해하고 글을 읽으시길 추천합니다. 긴 글이 부담스러우시면 요약 정리 부분부터 읽고 모르는 부분만 골라서 읽으셔도 좋습니다.
블로그에 시스템 프로그래밍의 다양한 랩들의 설명과 소스코드 뿐만 아니라 랩을 위한 기초 지식 글들을 게시하니, 즐겨찾기에 추가해두고 자주 찾아주시면 감사하겠습니다.
1. 문제 소개
문제는 CSAPP의 datalab으로 자주 출제되는 문제입니다. 문제는 "int형의 bit string에서의 1의 개수 세기"입니다. Lab session에서는 학교 별로 상이하지만, bitCount나 countOneBits 등의 함수를 구현으로 출제됩니다. 단순해보이지만 주의해야할 것은 if, do, while, for, switch와 같은 연산자 없이 문제에 따라 주어진 연산자만을 사용하여 문제를 해결합니다. 이 문제에서는 ! ~ & ^ | + << >> 만 허용됩니다 (legal operators). CSAPP datalab에서 제공되는 문항 다음과 같습니다.
/*
* bitCount - returns count of number of 1's in word
* Examples: bitCount(5) = 2, bitCount(7) = 3
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 40
* Rating: 4
*/
int bitCount(int x) {
// implementation
}
예시를 들어보자면 다음과 같습니다.
bitCount(0b10101010) : 0b10101010 이므로 4
bitCount(0b11001111) : 0b11001111 이므로 6
예시는 16비트의 간단한 문자열이지만, CSAPP datalab에서는 int형의 수를 다룰 것입니다.
2. 선형 알고리즘 (Linear Algorithm)
선형 알고리즘은 간단합니다. 1의 개수를 세는 것은 곧 전체 이진수의 각 자릿수의 합입니다. 따라서 저희는 LSB를 추출하여 cnt변수에 더하고, 주어진 수를 1회 right shift 할 것입니다. Right shift 덕분에 모든 비트를 LSB로 옮겨와 작업을 진행할 수 있습니다.
소스 코드는 다음과 같습니다.
int bitCount(int n)
{
int cnt = 0;
for(int i = 0; i < 36; i++){
cnt += n & 0x1; // LSB 추출 (masking)
n >>= 1; // right shift를 통해 모든 비트가 한 비트씩 이동
}
return cnt;
}CSAPP datalab 과제에서는 반복문을 사용할 수 없기 때문에 다음과 같이 구현해야합니다.
int bitCount(int n)
{
return (n >> 0 & 0x1) + (n >> 1 & 0x1) + (n >> 2 & 0x1) + (n >> 3 & 0x1) + (n >> 4 & 0x1) + (n >> 5 & 0x1) + (n >> 6 & 0x1) + (n >> 7 & 0x1) + (n >> 8 & 0x1) + (n >> 9 & 0x1) + (n >> 10 & 0x1) + (n >> 11 & 0x1) + (n >> 12 & 0x1) + (n >> 13 & 0x1) + (n >> 14 & 0x1) + (n >> 15 & 0x1) + (n >> 16 & 0x1) + (n >> 17 & 0x1) + (n >> 18 & 0x1) + (n >> 19 & 0x1) + (n >> 20 & 0x1) + (n >> 21 & 0x1) + (n >> 22 & 0x1) + (n >> 23 & 0x1) + (n >> 24 & 0x1) + (n >> 25 & 0x1) + (n >> 26 & 0x1) + (n >> 27 & 0x1) + (n >> 28 & 0x1) + (n >> 29 & 0x1) + (n >> 30 & 0x1) + (n >> 31 & 0x1) + (n >> 32 & 0x1) + (n >> 33 & 0x1) + (n >> 34 & 0x1) + (n >> 35 & 0x1) + (n >> 36 & 0x1);
}Datalab에서는 연산자 조건 때문에 조건에 맞지 않을 뿐더러 효율적이지 못한 방법입니다. 이분탐색을 기반으로한 3. Neighbor Counting과 4. Cross Counting를 통해서 연산수를 줄이는 방법을 소개하도록 하겠습니다.
3. Neighbor Counting
3.1 알고리즘 개요
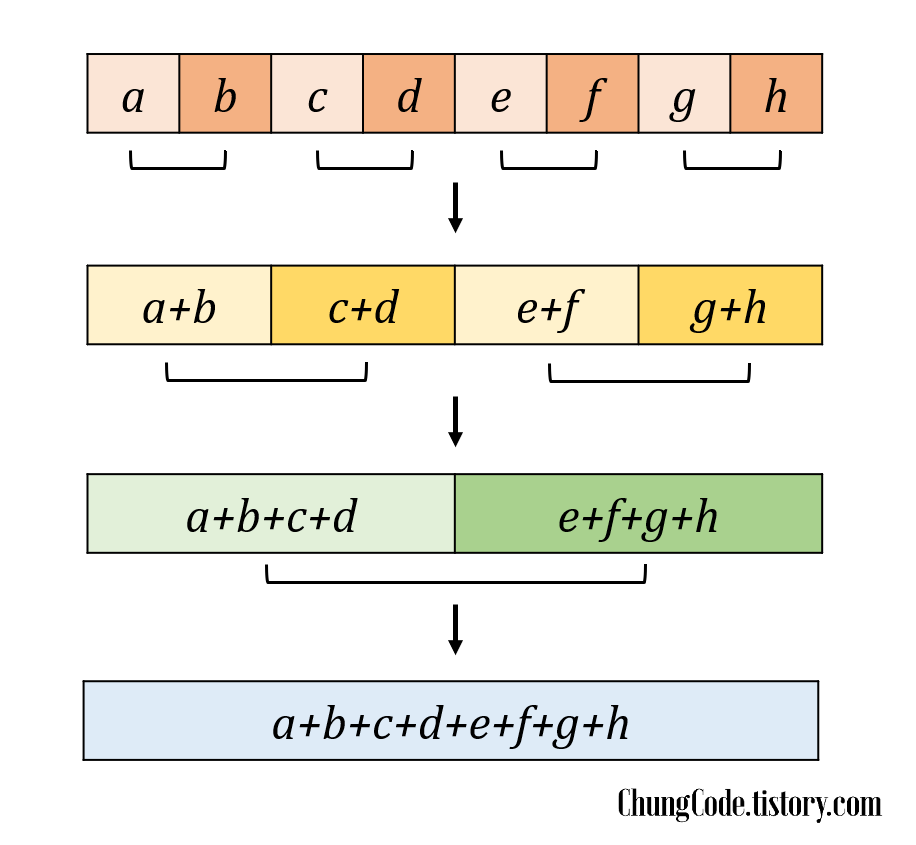
Neighbor counting 알고리즘은 이진 탐색을 기반으로 한 비트를 세는 알고리즘 중 하나입니다. 아래의 figure1을 함께 보면서 이해해주시면 됩니다. 아래와 같은 8bit의 bit string을 통해서 이해를 해보도록 하겠습니다. MSB부터 LSB까지 차례대로 비트가 나타내는 수가$ a, b, c, d, e, f, g, h $라고 하겠습니다. 우리는 최종적으로 $ a+b+c+d+e+f+g+h $ 의 값을 얻어야 합니다. 이때 각 비트를 독립적인 block이라는 단위로 지칭하겠습니다. 처음에는 $ [a] [b] [c] [d] [e] [f] [g] [h] $ 와 같이 블록이 형성되어 있습니다. 그러면 먼저 이웃한 두개의 블록끼리 더하는 작업을 진행하여 $ [a+b] [c+d] [e+f] [g+h] $와 같은 독립적인 블록을 형성합니다. 같은 방법으로 이웃한 두 블록씩 더하면$ [a+b+c+d]$ 와 $ [e+f+g+h] $ 블록을 형성합니다. 한 번 더 이웃한 블록씩 더하게 되면 $ [a+b+c+d+e+f+g+h] $ 블록을 형성합니다. 이 방법이 Neighbor Counting 방법입니다.
3.2 단계별 설명
대략적인 알고리즘은 위와 같고, 조금 더 자세히 어떤 연산들을 통해 실현되는지 알아보겠습니다.
Figure1의 1, 2, 3 과정은 마스크1를 통해서 이루어집니다. 처음에 이웃하는 두 개의 블록끼리 병합할 때를 살펴봅시다. 숫자를 더하기 위해서는 두 개의 시행이 필요함을 관찰할 수 있습니다. 첫번째는 자릿수 맞추기, 두 번째는 더하고자 하는 수만 남기는 필터링 입니다. 첫번째 iteration을 분석해보겠습니다.
- 자릿수 맞추기는 right shift operation을 통해서 실현됩니다. n과 n>>1을 통해서 더하고자 하는 블록끼리의 자릿수를 맞출 수 있습니다.
- 더하고자 하는 수만 남기기 위해서는 bitwise AND operation과 mask를 사용합니다. 우리는 짝수 비트의 블록만 남겨야 하기에 그림과 같이 0b01010101 의 마스크를 생성합니다. $ n \:\&\: mask1,\; n >> 1 \:\&\: mask1 $로 마스크를 적용하면, $ [-] [b] [-] [d] [-] [f] [-] [h]$ 와 $ [-] [a] [-] [c] [-] [e] [-] [g]$를 형성합니다. 사실 mask를 통해서 원하는 수 외의 블록은 0으로 처리했기에 $[ b ] [ d ] [ f ] [ h ]$와 $[ a ] [ c ] [ e ] [ g ]$ 로 보는게 정확합니다. 즉, 1회 iteration이 진행되면 그 크기가 확장됩니다.
두 과정을 거친 두 수를 더하면 이웃한 두 블록끼리 더한 $[a+b] [c+d] [e+f] [g+h]$ 를 얻을 수 있습니다.
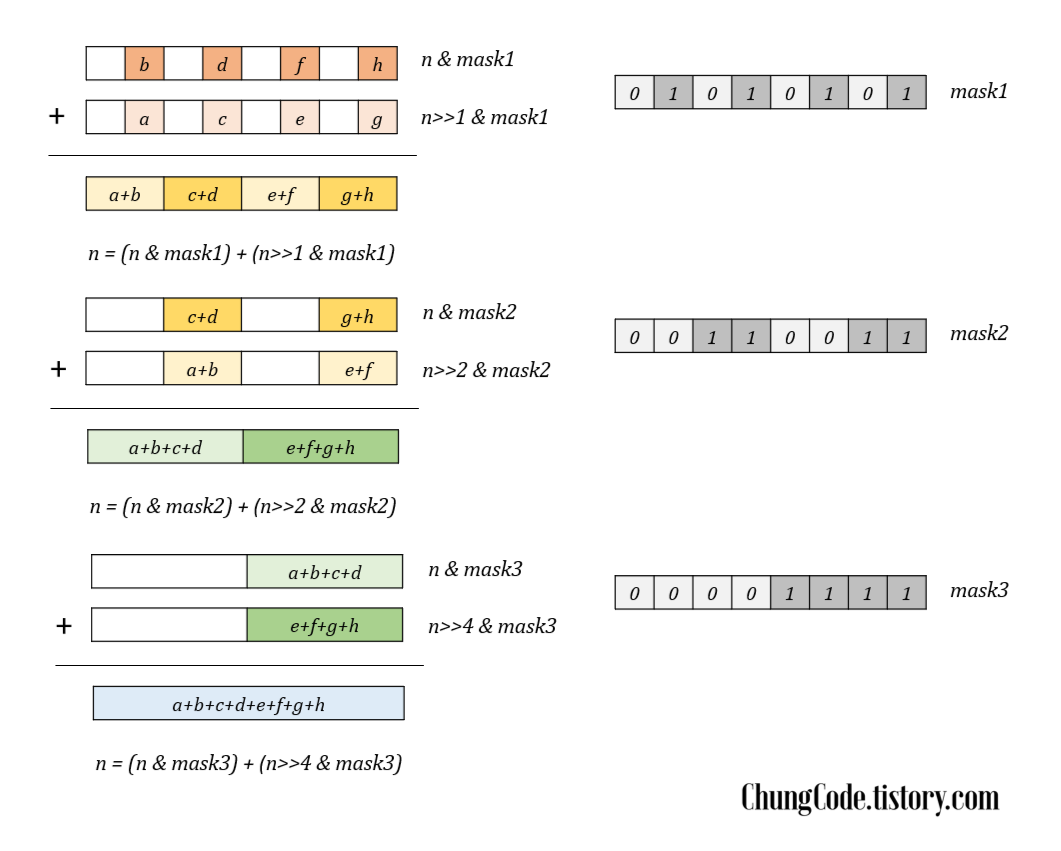
이 과정을 블록 크기가 $n$의 bit수가 될 때 까지 반복합니다. 반복하여 $[a+b+c+d]$ 와 $[e+f+g+h]$과 $[a+b+c$ $+d +e+f+g+h]$를 얻을 수 있습니다. 이때 위 방법과 달라지는 것은 right shift operation을 몇 칸 하는지와 mask의 형태입니다. Right shift operation은 새로 형성된 블록의 크기만큼 진행하면 됩니다. mask는 똑같이 짝수 블록만 남도록 설계하면 됩니다. 예를 들어 두번째 과정에서는 블록의 크기가 2이기에 shift가 2bit 진행되었고, 마스크는 블록만 filtering할 수 있도록 0b00110011의 형태를 띕니다. 세번째 과정에서는 블록의 크기가 4이기에 shift가 4bit 진행되었고, 마스크는 블록만 filtering할 수 있도록 0b00001111의 형태를 띕니다. 구체적으로 이야기하면 블록의 크기가 $w$이면 $0$를 $w$개, $1$를 $w$개, $0$를 $w$개, $1$를 $w$개 ...를 반복하면 됩니다.
3.3 소스 코드
int maskGenerate(int w, int intsize)
{
int mask = 0;
for(int i = 0; i < intsize / w / 2; i++){
mask <<= w; // 앞에 0를 w 만큼 붙이기
for(int j = 0; j < w; j++)
mask = (mask << 1) + 1; // 그 다음에 1을 w만큼 붙이기
}
return mask;
}
int bitCount(int n)
{
int w = 1, intsize = 32, mask;
while(w < intsize){
mask = maskGenerate(w, intsize); // 블록 크기에 따른 마스크 제작
n = (n & mask) + (n >> w & mask); // 덧셈을 위한 자릿수 맞추고 마스크를 통한 필터링
w <<= 1; // 블록이 합쳐졌기에, 블록 크기 변수를 두 배로 늘리기기
}
return n;
}앞서 설명한 알고리즘을 그대로 구현했습니다. maskGenerate 부분은 $w$이면 $0$를 $w$개, $1$를 $w$개, $0$를 $w$개, $1$를 $w$개 ...를 반복한 꼴이므로 자세한 구현은 크게 신경쓰지 않으셔도 됩니다. bitCount함수에서는 초기 블록 크기 $w$를 1로 설정하고, int가 32비트임을 변수에 기록했습니다. 다른 과정들은 위 알고리즘과 일치하니 잘 이해가 되지 않으시면 3.3과 Figure2를 참고하시면 좋을 것 같습니다.
Datalab에서는 마스크를 직접 선언하고, 반복되는 작업을 한 줄씩 입력하면 됩니다.
3.4 장단점
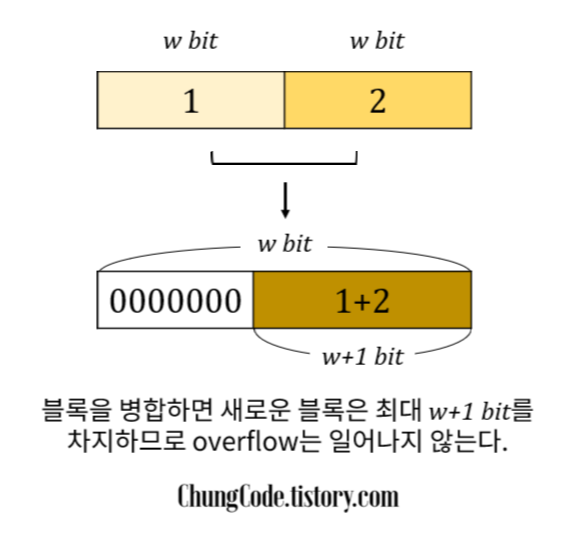
이 알고리즘의 장단점을 소개하겠습니다. 장점은 블록의 크기의 제한이 없습니다. 이는 cross counting에 비교하여 큰 장점입니다. 예를 들어 블록의 크기가 $w$인 두 블록을 병합한다고 합시다. 두 블록의 자릿수를 맞춘 후 mask를 통해서 유효하지 않은 부분은 모두 0으로 만듭니다. 이후 블록을 병합하면 크기가 $2w$인 블록이 만들어집니다. 우리는 각각 $w$bit인 두 수, 즉 $2^w-1$을 표현하는 두 수를 더해서 이를 $2w$bit에 넣은 것이나 마찬가지입니다. $2^{2w} \geq 2(2^w - 1)$이므로 우리는 비트를 병합할 때 항상 overflow없이 block에 안전하게 담을 수 있습니다. (담긴 수는 2배 커지는데 담는 공간은 $2^w$ 증가한다고 이해하면 쉽겠습니다.) 이후에 알아볼 cross counting은 이러한 특징을 가지지 않습니다.
단점은 구현이 cross counting보다 까다로울 수 있습니다. 각 상황에 따라서 마스크를 만들어줘야하는 불편함이 있습니다. 이 마스크도 생성 규칙이 존재하지만, 이러한 까다로움이 없는 cross counting과 비교했을 때 분명한 단점입니다. Datalab구현 시에도 operation수 제한 이 때문에 문제가 발생할 수 있는데 이는 lab sesssion 설명 게시물에서 자세히 알아보도록 하겠습니다.
4. Cross Counting
4.1 알고리즘 개요
Cross counting 알고리즘 역시 이진 탐색을 기반으로 한 비트를 세는 알고리즘입니다. Neighbor counting과 똑같이 블록을 병합하면서 수를 더한다는 공통점이 있습니다. 하지만 두 알고리즘의 초기 상태가 조금 다릅니다. neighbor counting이 처음 블록 크기가 1인 상태에서 시작했지만, cross counting은 그러할 수 없습니다. 그 이유를 알고리즘과 함께 이해하면 좋습니다.
아래의 Figure4를 참고하면서 이해하면 좋습니다. 예시의 블록들은 모두 8비트이고. 초기 상태에서 각각의 블록은 초기의 1~8, 9~16, 17~24, 24~32 비트의 1의 개수를 계산해둔 상태 2 입니다. 아래 예시에서는 각각 $ 5, 2, 7, 3 $으로 계산되어있습니다. 짝수는 짝수 블록끼리, 홀수는 홀수 블록끼리 더해주고 더한 두 블록 중 오른쪽에 가까운 블록에 저장하는 작업을 반복합니다. 첫번째 iteration에서 $z$에 $A+C$의 값을를 저장하고 $w$에 $B+D$를 저장합니다. 그러하면 좌측 두 $x,\:y$블록은 그대로이고 우측의 $z,\:w$ 두 블록만 갱신됩니다. 다음 iteration에도 같은 작업을 $z,\:w$에 대해서 시행하여 $w$에 $(A+C)+(B+D)$를 저장합니다. 마지막으로 $x,\:y,\:z$에 있는 garbage value들을 제거해주면 됩니다.
4.2 단계별 설명
짝수는 짝수 블록끼리, 홀수는 홀수 블록끼리 더해주고 더한 두 블록 중 오른쪽에 가까운 블록에 저장하는 작업만 반복해서 진행하면 됩니다. 이는 right shift operation으로 실현됩니다. 처음에는 $n \& (n >> 2)$를 진행하지만, 정보가 있는 블록의 수가 절반이 되었기에 다음에는 $ n \& (n >> 1) $ 을 진행합니다. Bit shifting으로 만들어진 garbage value들은 블록 크기의 값들만 통과시키는 mask를 통해 제거됩니다.
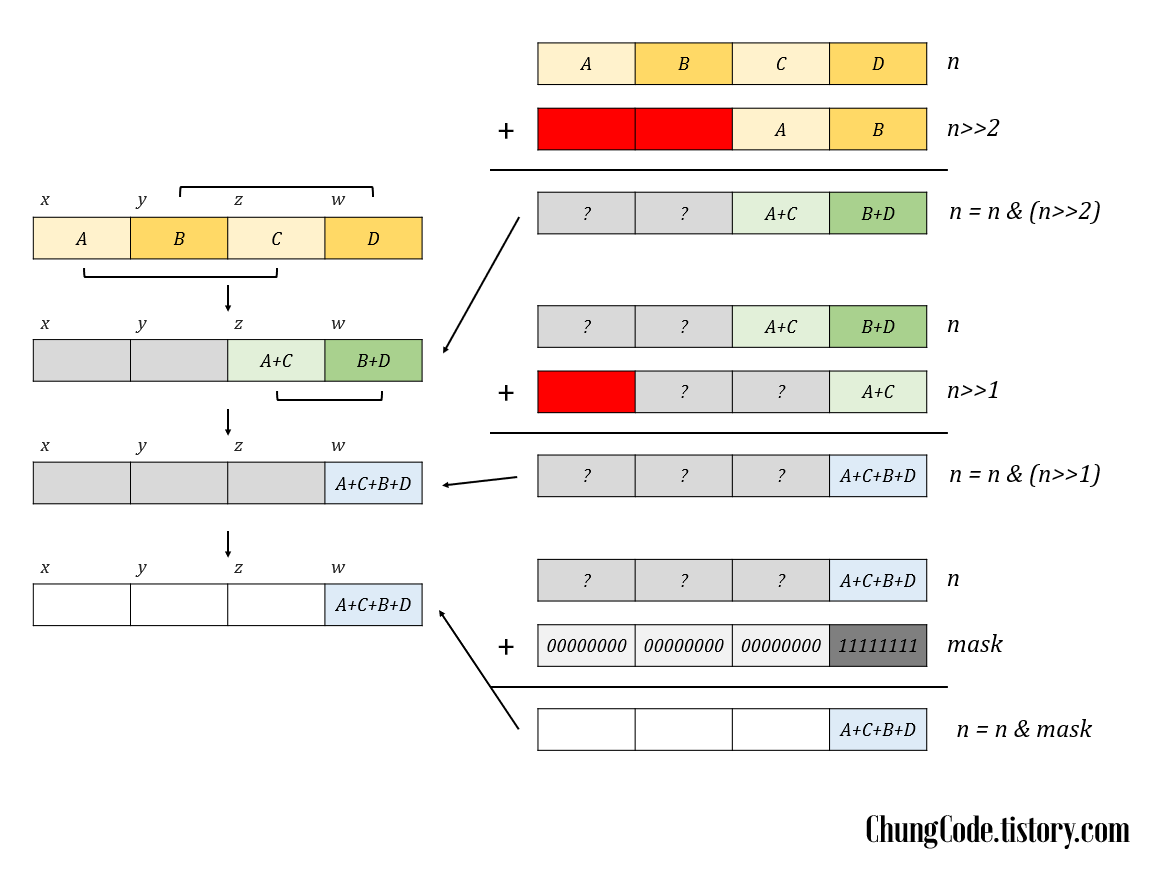
마지막 단계를 살피면 총 비트수가 하나의 블록에 담깁니다. 그렇기 때문에 최초 블록의 크기를 설정할 때, 최대 가능 비트수가 한 블록에 담길 수 있는지를 고려해야합니다. 최대 가능 비트수가 $n\:bit$라면 블록의 크기 $w$는 $logn$보다 커야 합니다.
(블록이 표현할 수 있는 최대 수: $2^w - 1$) $\geq$ (최대 가능 비트: $n$)
$ \Rightarrow $ $w>logn$
블록의 크기가 성장하지 않고, 처음에 지정한 블록의 크기에 모든 정보가 담긴다는 측면에서 Neighbor Counting과 차이가 있습니다. 따라서 블록을 $w>logn$ 조건에 맞게 크기를 설정해야합니다.
4.3 소스 코드
#include <stdio.h>
int bitCount(int n)
{
int intsize = 32, w = 8;
int shiftnum = intsize / 2; // 처음에 총 비트의 절반을 이동해야 합니다.
while(shiftnum >= w){
n = n + (n >> shiftnum); // cross counting
shiftnum >>= 1; // 16 -> 8 이런식으로 감소합니다.
}
n = n & 0xFF; // 8비트 블록 마스킹
return n;
}
int main()
{
printf("%d",bitCount(0x05020703));
return 0;
}일반적인 코드는 가독성을 떨어트려 위 예시와 같은 상황에서 작동하도록 구현했습니다. 블록의 크기는 8입니다.
CSAPP랩의 legal operation에 맞추어 bitCount 또는 countOneBits라고 불리며, 테스트를 통과하려면 이 링크를 클릭하면 자세히 볼 수 있습니다. 다른 문제의 해설도 있으니 countOneBits 외에도 다른 문제의 해답도 확인하세요.
4.4 장단점
Cross counting은 neighbor counting과 비교하여 iteration마다 마스크를 생성할 필요 없이 shift 이후 더하면 됩니다. 그러나 단점으로는 초기 상태가 비트의 수를 계산해둔 블록이라는 점입니다. $w>logn$ 조건 때문에 neighbor counting과 같이 블록의 크기가 1인 상태에서 시작할 수 없습니다. 따라서 $w>logn$ 를 만족하는 블록을 미리 형성하기 위해 linear algorithm이나 cross counting을 꼭 병행해서 사용해야합니다.
5. 정리
| Neighbor Counting | Cross Counting | |
| 블록의 크기 변화 | 증가 | 일정 |
| 초기 블록 크기 ($w$) | 자유로움 | $w>logn$ |
| 준비물 | 각 iterarion에 필요한 마스크 | 블록 크기에 맞춰 비트 수 블록들 |
| 시간 복잡도 | $O(logn)$ | $O(logn)$ |
본문에서 다루지 않았지만 두 알고리즘의 시간 복잡도는 모두 $O(logn)$ 입니다.
이 글의 코드들은 반복문으로 작성되어, 실제 Datalab에서 위 세 알고리즘을 모두 사용할 수 있습니다(linear algorithm은 연산자 제한으로 단독으로 사용할 수 없습니다.)
오늘 글은 여기에서 마치겠습니다. 궁금하신 점은 댓글을 달면 언제든지 답변해드립니다. 블로그에 시스템 프로그래밍의 다양한 랩들의 설명과 소스코드 뿐만 아니라 랩을 위한 기초 지식 글들을 게시하니, 즐겨찾기에 추가해두고 자주 찾아주시면 감사하겠습니다. 좋아요와 응원 댓글은 큰 힘이 됩니다.